Neural Collaborative Filtering(NCF)

들어가기 전에 - Recommendation System이란 무엇인가?

추천 시스템은 간단히 말해서 정보를 필터링해주는 도구라고 할 수 있다. 수 많은 종류의 선택지 중에서 유저에게 가장 적합하거나 흥미있어 할만한 후보들을 제시해 주는 것이다. 위키피디아의 정의에 따르면 추천 시스템은 정보 필터링 방식의 한 종류로 유저가 아이템에게 줄 것 같은 “rating” 이나 “preference”등을 예측하는 것이다.

이러한 유저와 아이템 간의 관계를 표현하기에 유용한 방법 중 하나가 바로 Matrix(행렬)이다. 각각의 행을 user, 열을 item으로 놓는다면 각 user가 item에 대해서 어떻게 평가(rating)했는 지를 쉽게 표현할 수 있다. 예를 들어, 영화에 대한 각 유저의 rating을 matrix로 표현하면 아래의 그림과 같다.

수 많은 유저와 아이템으로 구성된 행렬을 생각해보면, 행렬의 대부분의 공간은 비어있다는 것을 쉽게 알 수 있다. 수 많은 아이템 중에서 한 명의 유저가 실제 소비하는 아이템은 극히 일부분일 것이기 때문이다.

추천시스템의 목적은 이러한 User-Item matrix의 비어있는(sparse한) 공간의 값을 예측값으로 채워넣는 것이다.

---

Introduction

오늘 다루고자 하는 논문은 WWW 2017에 발표된 Neural Collaborative Filtering이라는 논문이다. 본 논문에서 목표로 하는 것은 두가지이다.

• implicit feedback을 사용해서 user들에게 item을 추천해주는 것
• matrix factorization의 user-item interaction 부분을 deep learning을 사용해서 개선하는 것

이 두 목표에 대해 이해를 하려면 먼저 implicit feedback과 matrix factorization이 무엇인지 알아야 한다.

Implicit Feedback

Implicit feedback은 user의 preference를 user의 지난 behavior로부터 indirect하게 유추할 수 있도록 해준다. 넷플릭스에서 영화를 클릭해서 시청을 한다거나, 아마존에서 제품의 상세를 보기 위해 클릭을 하는 행동 모두 implicit feedback에 해당한다. 이와 반대의 개념인 explicit feedback은 user가 직접 특정 영화에 대해 평점을 매기거나 상품 후기를 남기는 행동들을 말한다.

Implicit feedback은 explicit feedback와는 다르게 선호도를 물어볼 필요가 없으므로 자동적으로 수집이 되며, 모으기도 쉽다. 하지만 User의 만족도를 나타내는 signal이 아니므로 사용하기는 더 까다롭다.

User-Item martix로 나타낼 경우, user와 item사이에 interaction이 있으면 1, 그렇지 않으면 0의 값으로 채워 넣을 수 있다. 여기서 1이라는 값이 user가 실제로 item을 좋아한다는 것을 말하지는 않고, 마찬가지로 0이라는 값이 user가 item을 싫어한다고 볼 수는 없다. 오히려 user가 item을 모르고 있는 상태라고 할 수 있다.

Matrix Factorization

여기서 matrix factorization의 기본 개념들을 모두 다룰 수는 없고(추후에 자세하게 다뤄볼 예정), 이 논문에서 deep learning을 사용하여 어떤 부분을 개선하고자 했는 지에 초점을 두고 설명할 것이다.

Matrix factorization이라는 기법은 user와 item을 동일한 latent space 상에 투영하는 것이라고 볼 수 있다. 즉, user와 item을 latent feature vector로 표현하고, 두 latent feature의 상호작용을 모델링하는 것이다. 이를 좀 더 알기 쉽게 그림으로 표현하면 아래와 같다.

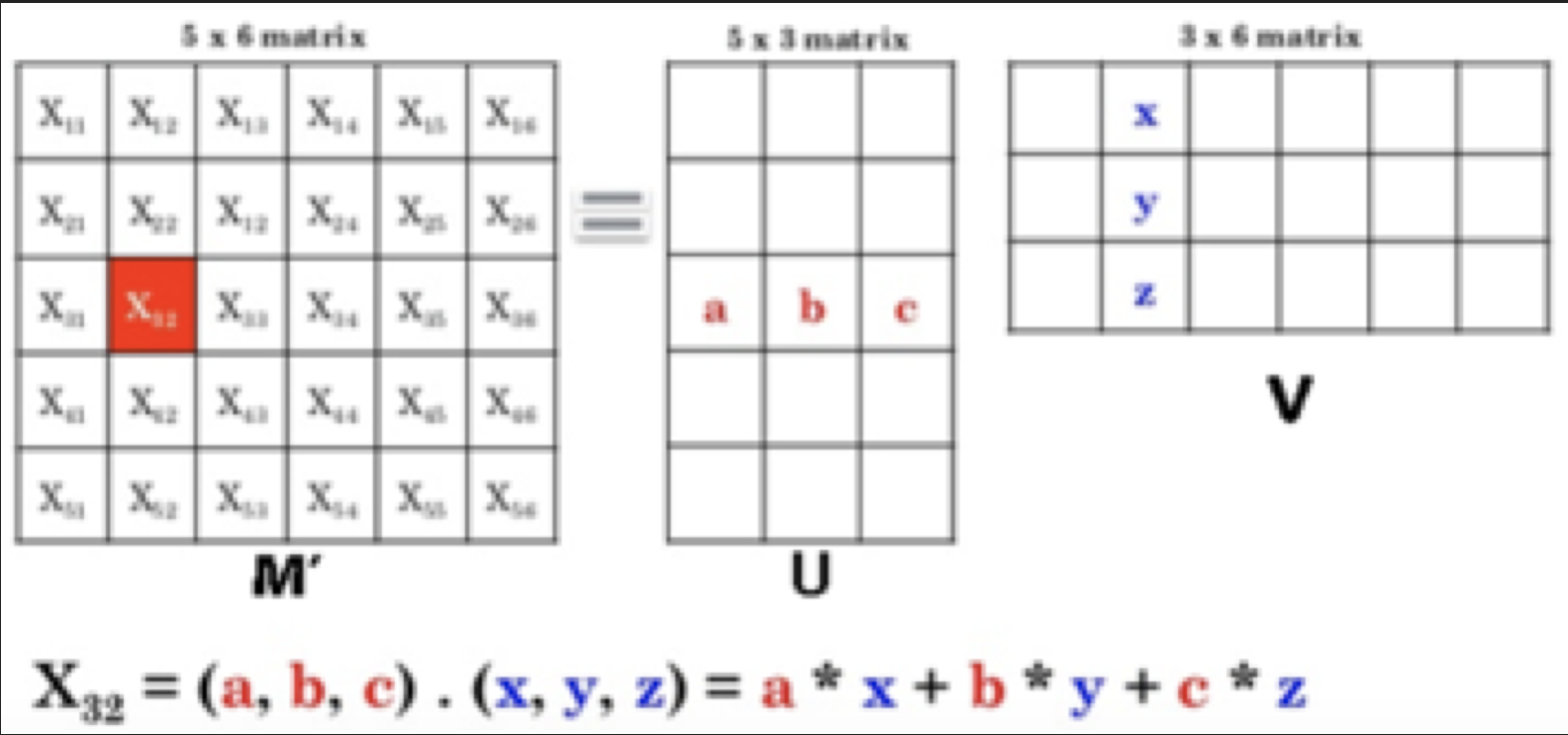
특정한 user u는 (a,b,c) 라는 vector로 표현되고, item i는 (x,y,z)라는 vector로 표현할 수 있다. matrix factorization은 이 둘 간의 interaction을 inner product로 정의하여 score를 계산한다.

이 논문은 여기서 문제를 제기한다. user와 item을 같은 latent space상에 project하기 때문에 둘의 interaction은 linear할 수 밖에 없고, 따라서 complex한 structure를 표현하기에는 부족하다는 것이다. 다시 말하면, interaction function을 더 잘 modeling하면 더 나은 성능을 낸다는 것이다.

이를 논문에서는 아래의 figure를 사용하여 설명하고 있다.

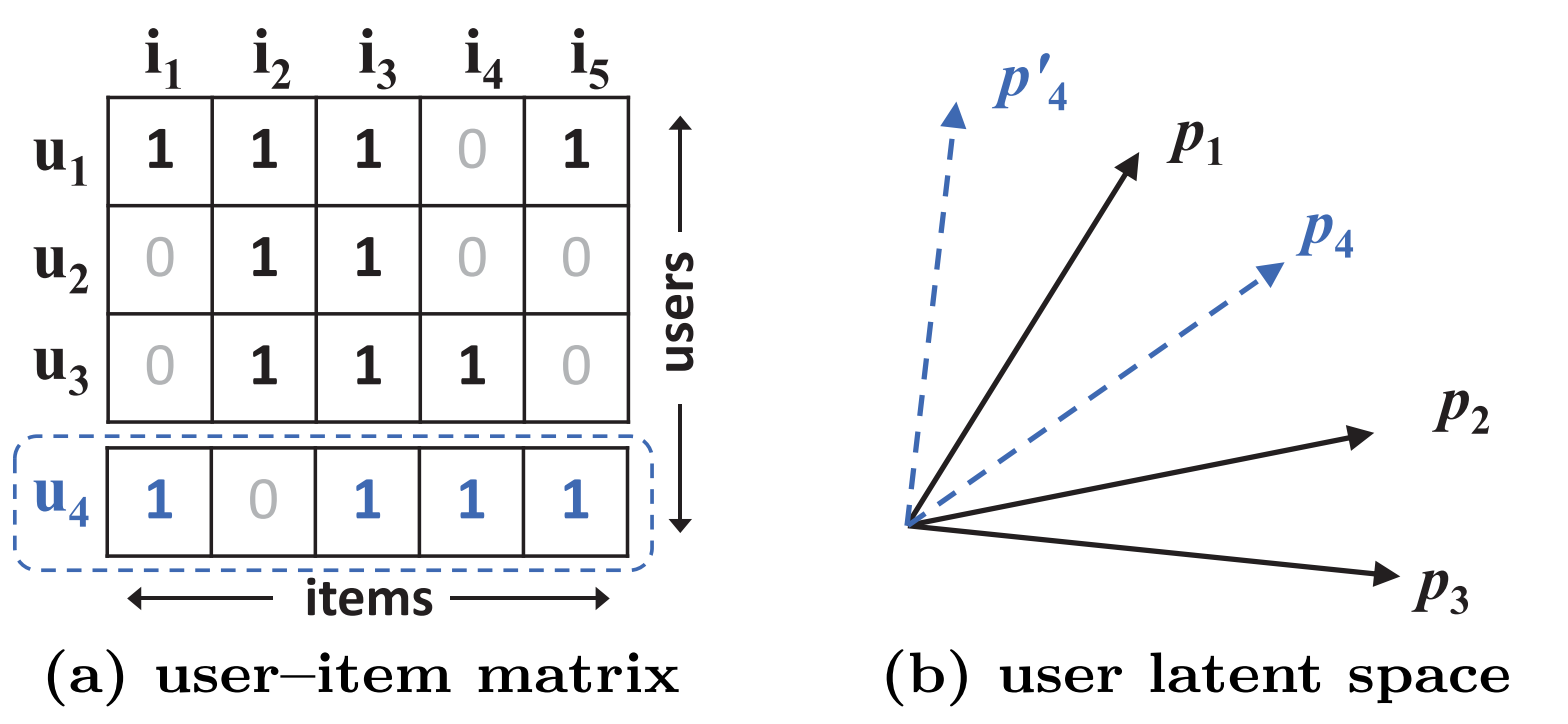
u1, u2, u3의 user가 현재 시스템에 있고, 각각의 user를 latent space상에서 나타내면 (b)의 검은 실선과 같다. 이후 u4가 새로 유입이 되었을 때, vector 간의 거리를 계산해보면 u1 > u3 > u2의 순으로 가깝지만 오른쪽의 latent space 상에서는 어떻게 해도 이를 나타낼 수가 없다.

이를 해결하기 위해서는 latent factor K의 크기를 늘릴 수 있지만, overfitting 되기 쉽다는 문제가 있다. 논문에서는 DNN을 사용하여 interaction function을 모델링하는 방법을 제시하고 있다.

---

Neural Collaborative Filtering Framework

논문에서는 General NCF Framework라는 구조를 소개하고 있다. 이 구조를 사용하면 matrix factorization도 표현할 수 있고, 더 나아가 multi-layer perceptron을 사용해서 non-linear한 모델도 표현할 수 있다. 결론부터 말하자면, 이 논문에서는 linear한 모델인 MF와 non-linear 모델인 MLP를 앙상블해서 성능을 향상시켰다.

General NCF Framework는 아래와 같은 구조로 이루어져 있다.

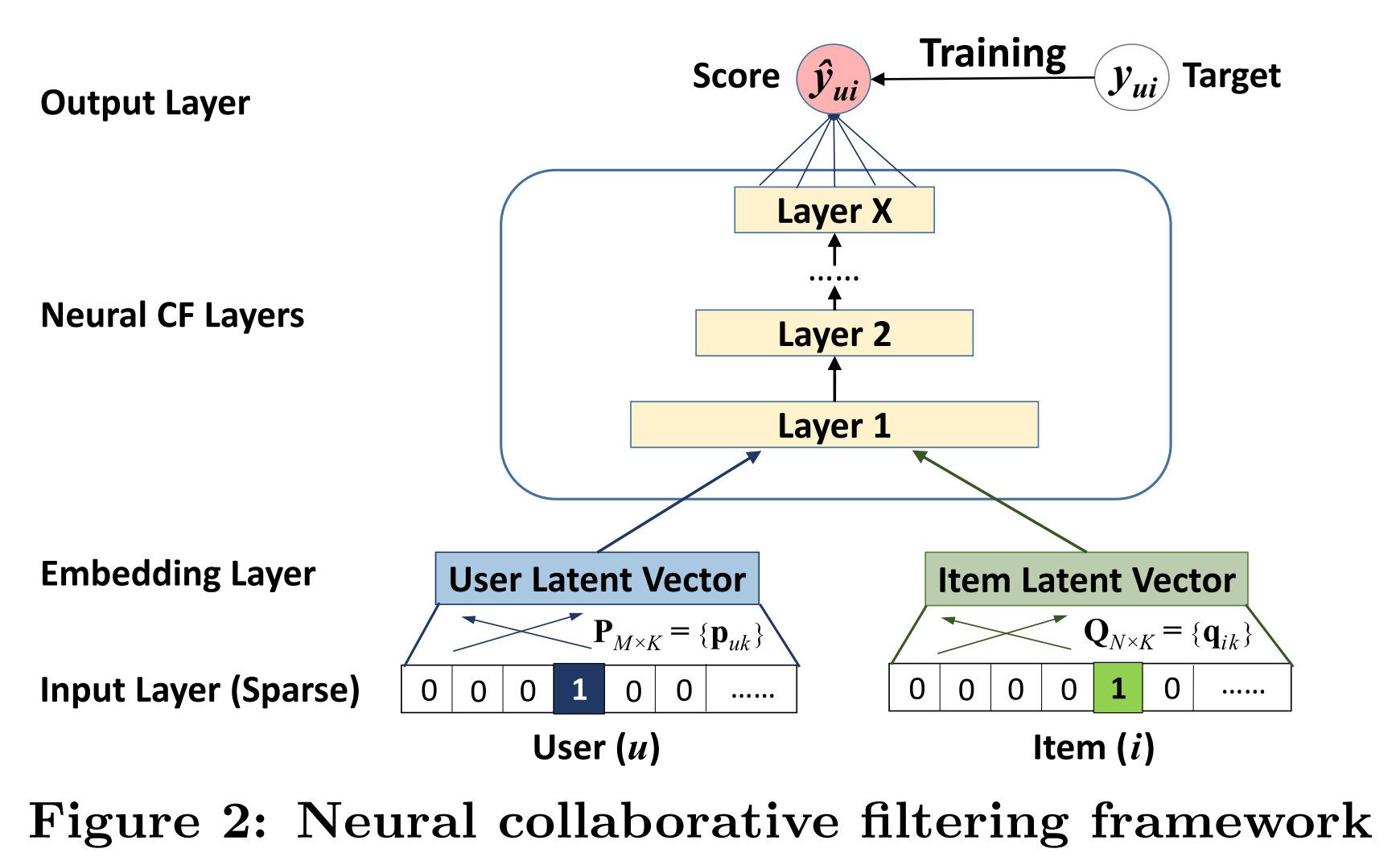
• Input layer
  • One-hot encode되어 있는 binarized sparse vector
  • User와 item에 대해 각각 다른 input 사용
• Embedding layer
  • FC layer를 사용하여 sparse representation을 dense vector로 변환
• Neural CF layer
  • multi-layer representation을 사용하여 user-item interaction을 modeling
  • latent vector를 prediction score로 mapping
  • 마지막 hidden layer X의 dimension의 모델의 capability를 결정
• Output layer
  • Predicted score $\hat{y}_{ui}$
• Training
  • point-wise loss 및 pair-wise loss로 학습이 가능하지만 논문에서는 point-wise loss만 사용하여 학습

Learning NCF

이 논문에서는 보통의 point-wise loss들이 regression을 사용하는 것과는 달리, binary cross-entropy loss를 사용했다. user와 item의 interaction 여부에 따라 0,1로 값을 두고 log loss를 사용해서 학습을 하였고, 후에 서술될 실험에서 이에 대한 성능을 증명하였다.

\[L = - \sum_{(u,i)\in{}Y\cap{Y^-}} y_{ui}log\hat{y}_{ui} + (1 - y_{ui})log(1 - \hat{y}_{ui})\]

Optimizer로는 SGD를 사용하였고, unobserved interaction, 즉 user가 아직 알지 못하는 item을 negative sample로 사용하였다.

Generalized Matrix Factorization

앞서 user-item interaction을 linear한 모델과 non-linear한 모델을 앙상블해서 사용했다고 하였다. 이 단락에서는 linear한 모델을 먼저 살펴보도록 한다. 간단하게 말해서 linear한 모델은 이전과 같이 Matrix factorization을 사용한다. 차이점은 Matrix factorization을 앞서 언급한 NCF framework로 표현이 가능하고, 일반화 할 수 있다는 것이다. 이를 식으로 나타내면 아래와 같다.

\[\hat{y}_{ui}= a_{out}(h^T(p_u{\odot}q_i))\]

• $\odot$ 은 element-wise product
• $a_{out}$ activation function
• $ h^T $ 는 edge weight of the output layer

여기서 $ h^T $가 uniform vector이고, $ a_{out} $이 identity function이면 기존의 MF과 동일하다는 것을 알 수 있다. 논문에서는 $a_{out}$으로는 sigmoid function, $h$는 log loss를 사용해 학습하였다.

Fusion of GMF and MLP

MLP는 익히 알고 있는 MLP의 구조이므로 전체 모델에 포함된 수식으로 설명을 대체한다. 아래의 그림은 Neural Matrix Factorization Model의 전체 구조이다.

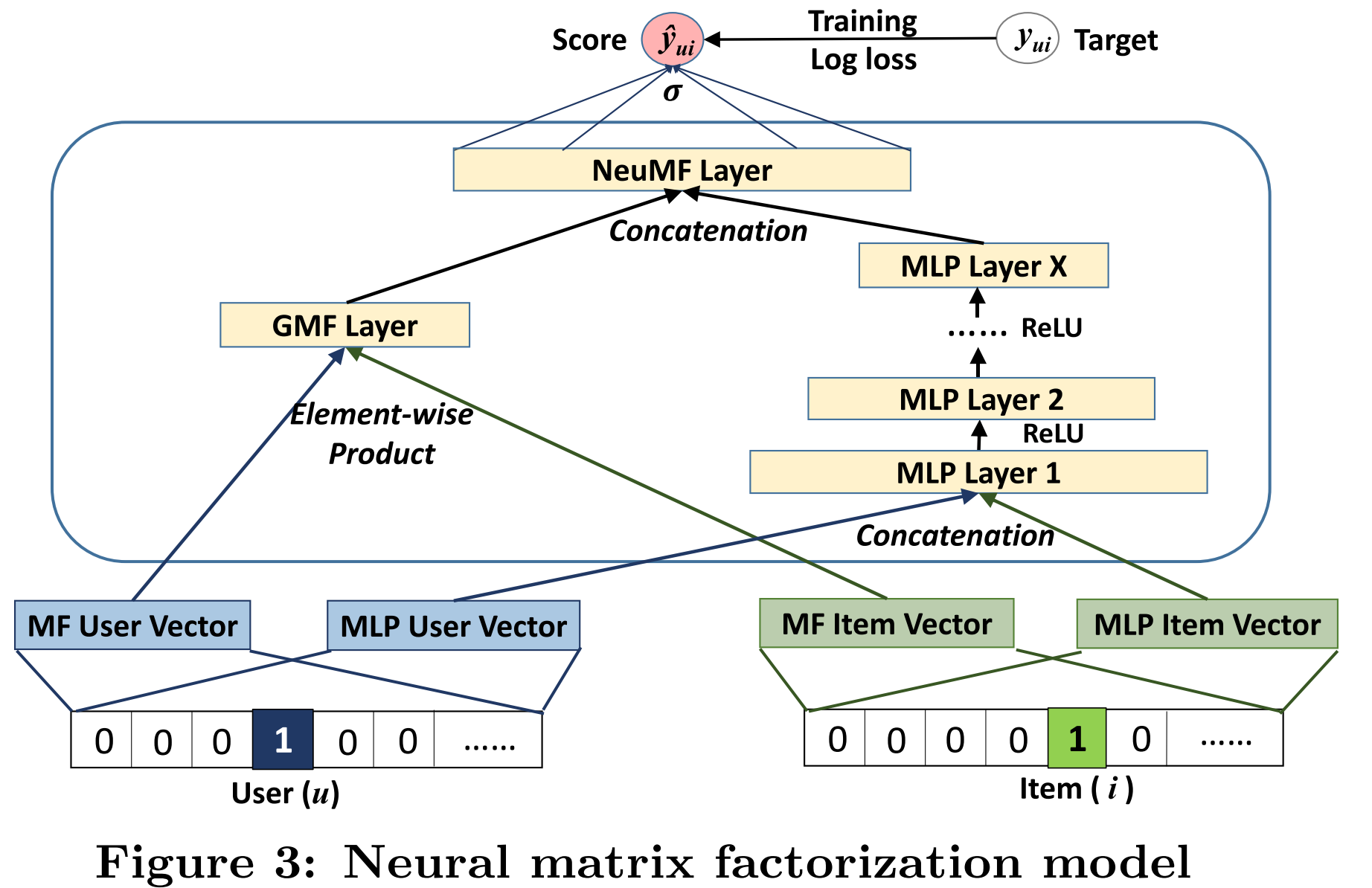
GMF Layer

• 앞서 다룬 GMF layer
  1. User와 item vector간의 element-wise product
  2. apply weight
  3. activation function

MLP Layer

• User와 item vector를 concatenate해서 사용
  • 좀더 flexible한 embedding 사용 가능
• MLP를 사용해서 “non-linear”한 interaction을 modeling
• activation function으로는 ReLU를 사용

NeuMF Layer

• GMF와 MLP layer를 fusion하는 단계
• GMF는 linear kernel을 사용하여 interaction function을 모델링
• MLP는 non-linear kernel을 사용
• 둘을 fuse하여 상호간에 reinforce해서 더 복잡한 interaction function을 모델링
• GMF/MLP layer의 output을 concat해서 input으로 사용
• Output으로는 User의 item에 대한 prediction score값을 출력

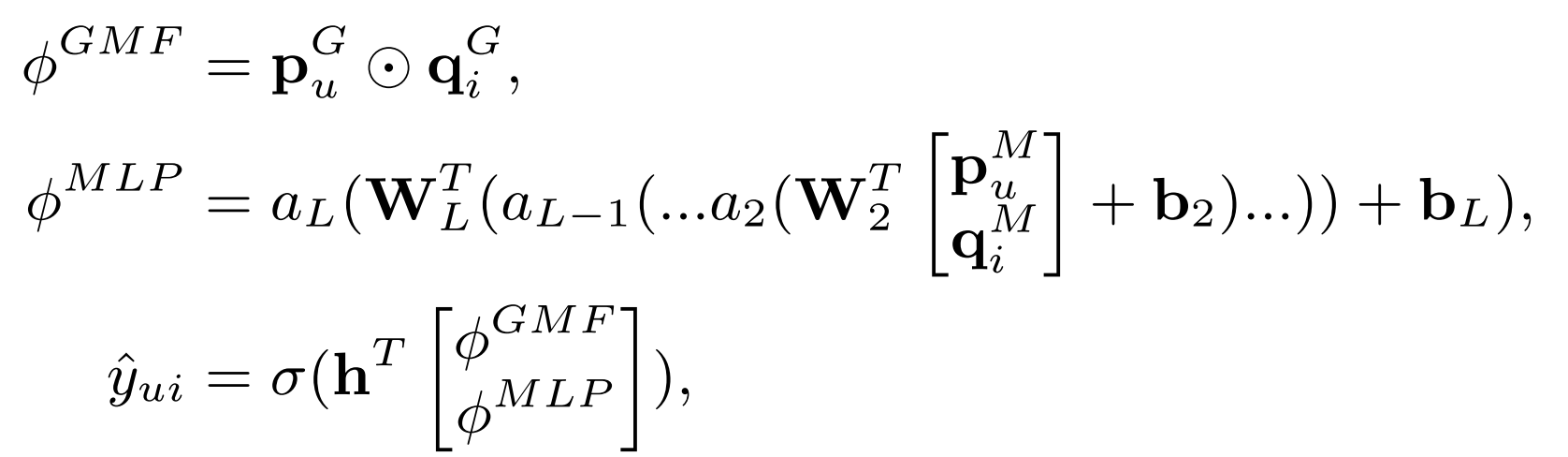
Training

• GMF와 MLP layer를 각각 먼저 pre-training한 다음 NeuMF를 학습
• GMF와 MLP는 ADAM optimizer를 사용하고 NeuMF에는 SGD 사용

Experiments

Experiments는 다음의 3가지 research question에 답을 하고 있다.

• Do our proposed NCF methods outperform the state-of-the-art implicit collaborative filtering methods?
  • Performance comparison
• How does our proposed optimization framework (log loss with negative sampling) work for the recommendation task?
  • Log loss with Negative sampling
• Are deeper layers of hidden units helpful for learning from user-item interaction data?
  • Is deep learning helpful?

Datasets

MovieLens와 pinterest의 dataset을 사용했으며, 최소 20개의 rating이나 pin을 남긴 user의 data만을 학습에 사용했다. 세부적인 구성은 아래와 같다.

비교를 위한 baseline으로는 ItemKNN, BPR, eALS 등을 사용했다.

RQ1. Performance Comparison

• 성능은 HR과 NDCG로 측정했는데, 당연히 NeuMF의 성능이 가장 좋다. 예상 밖이었던 것은 단일 모델 성능으로는 대부분의 경우에서 MLP보다 GMF의 성능이 좋다는 것이다.

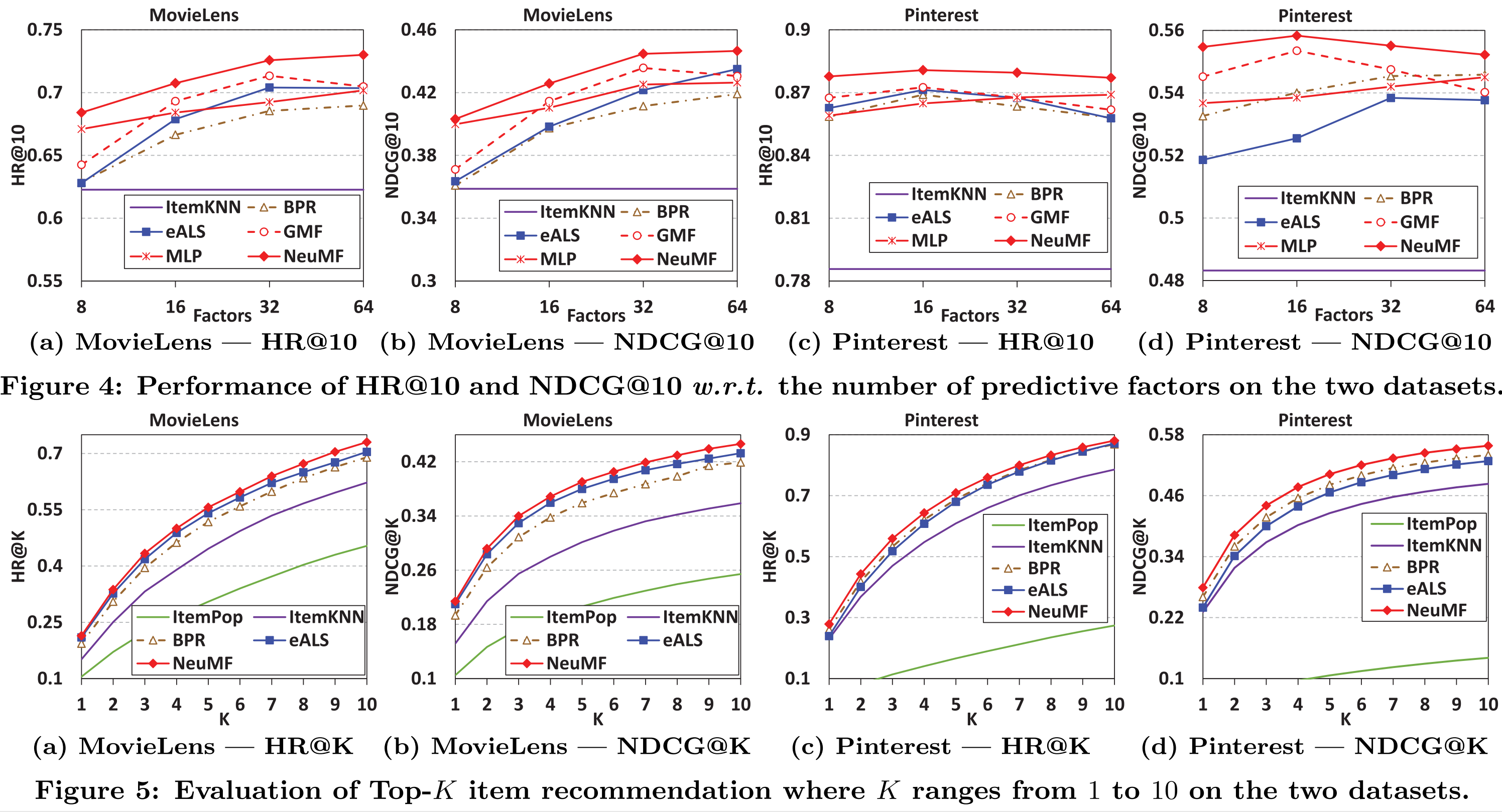
RQ2. Log loss with Negative Sampling’

• Loss가 줄어들 수록 성능이 증가하므로 log loss도 interaction function을 학습하는데 적절하다는 것을 알 수 있다.

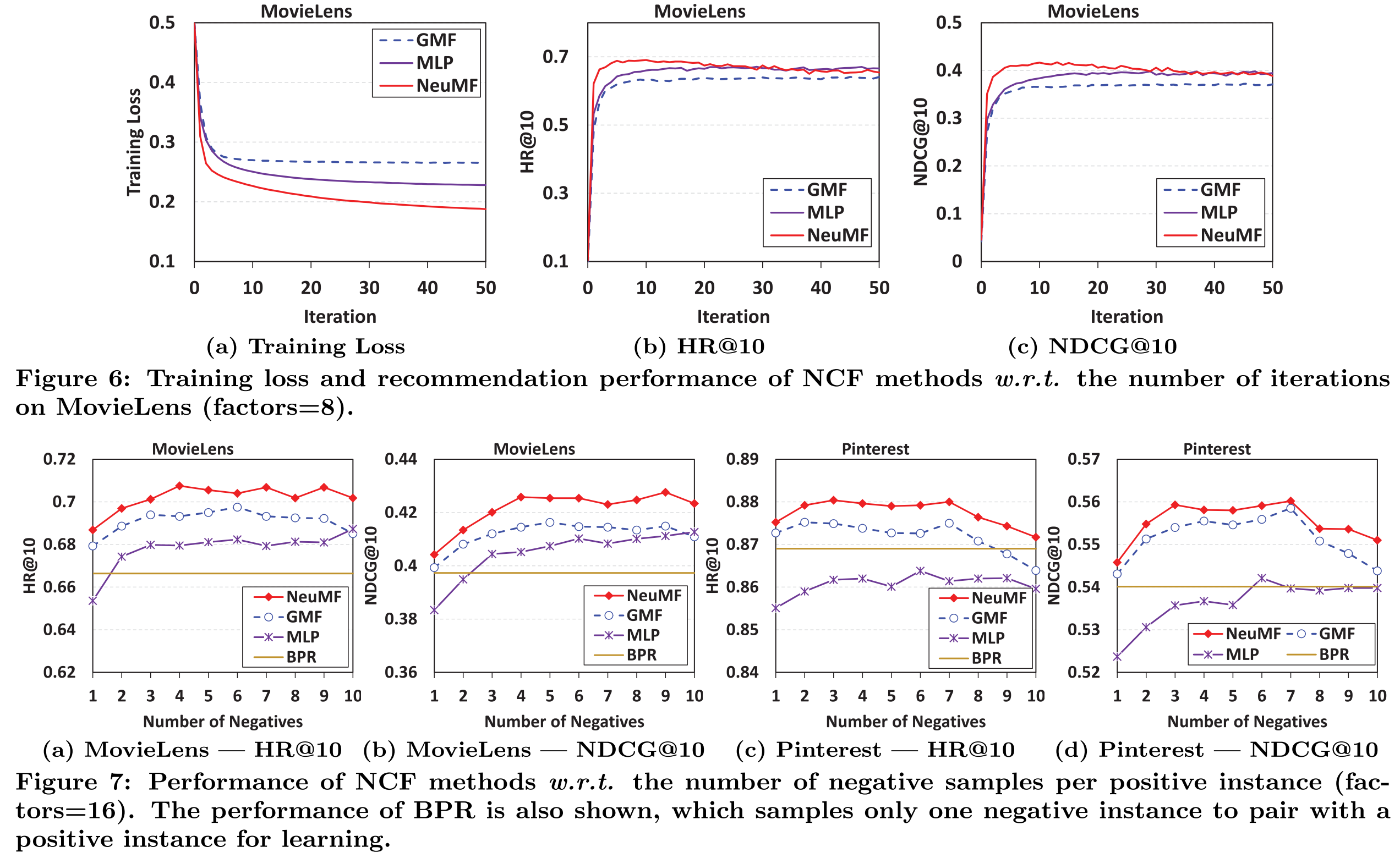
RQ3. Is deep learning helpful?

• Layer가 깊어질 수록 성능이 증가하므로, DNN이 성능에 도움이 된다고 할 수 있다.

---

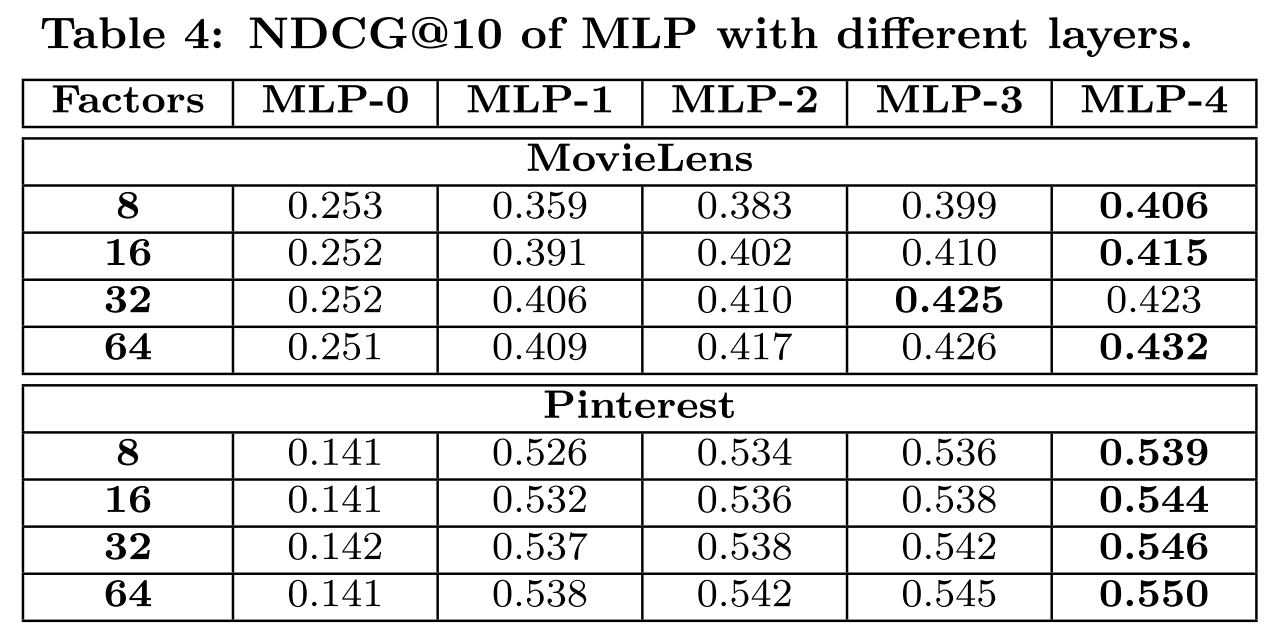
마치며

2020년 현재 deep learning을 사용하여 추천 시스템의 성능을 향상하려는 시도는 계속되고 있으며 괄목할 만한 결과물도 많다. 하지만 2017년의 이 논문은 deep learning의 아주 간단한 구조를 사용하면서도 우수한 성능을 보였고, 다른 논문의 근간이 되고 있으므로 필수적으로 알고 넘어가야 한다고 생각한다.

블로그에 가장 처음 적는 이글이 많은 분들에게 도움이 되었으면 좋겠습니다. 글 실력이 부족하여 혹 이해가 되지 않으셨다면 양해 부탁드립니다. 긴 글 읽어주셔서 감사합니다.

2020-05-15 00:00:00 +0000 - Written by Seho Kim